The correlation analysis refer to the techniques used measuring the closeness of the relationship between variables.
"Correlation analysis deals with the association between two or more variables."
1. Positive and Negative Correlation: whether correlation is positive or negative would depend upon the direction of change. i.e if as one variable is increasing the other, on an average is also increasing or if one variable is decreasing the other, on an average is also decreasing, correlation said to be positive. If on the other hand one variable is increasing, the other is decreasing or vice versa it is said to be negative correlation. e.g
1. Positive correlation:
X : 10 12 15 18 20 X: 80 70 60 40 30
Y : 15 20 22 25 37 Y: 50 44 30 20 10
2. Negative Correlation:
X: 20 30 40 60 80 X: 100 90 60 40 30
Y: 40 30 22 15 10 Y: 10 20 30 40 50
2. Linear and Non-Linear (Curvilinear) Correlation: The distinction between linear and non-linear correlation is based upon the constancy of the ratio of change between the variables. If the amount of change in one variable tends to bear constant ratio to the amount of change in the other variable then the correlation said to be linear.
Methods of Studying Correlation
1. Scatter Diagram
2. Karl Pearson Coefficient of Correlation
1. Scatter Diagram:
The more the points plotted are scattered over the chart, the lesser is the degree of correlation between the variables. The more the points plotted are closer to the line, the higher is the degree of correlation. The degree of correlation is denoted by “r”.
The following types of scatter diagrams tell about the degree of correlation between variable X and variable Y.
- Perfect Positive Correlation (r=+1): The correlation is said to be perfectly positive when all the points lie on the straight line rising from the lower left-hand corner to the upper right-hand corner.
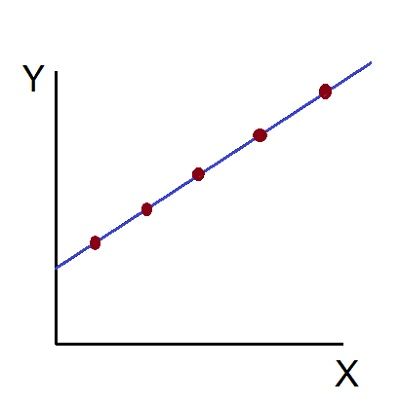
- Perfect Negative Correlation (r=-1): When all the points lie on a straight line falling from the upper left-hand corner to the lower right-hand corner, the variables are said to be negatively correlated.
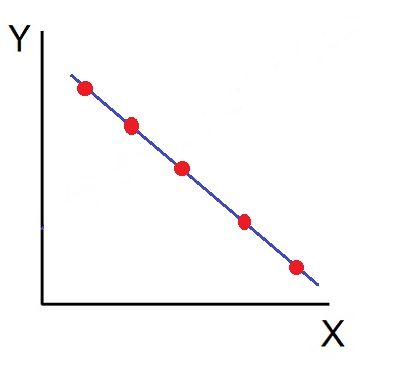
- High Degree of +Ve Correlation (r= + High): The degree of correlation is high when the points plotted fall under the narrow band and is said to be positive when these show the rising tendency from the lower left-hand corner to the upper right-hand corner.
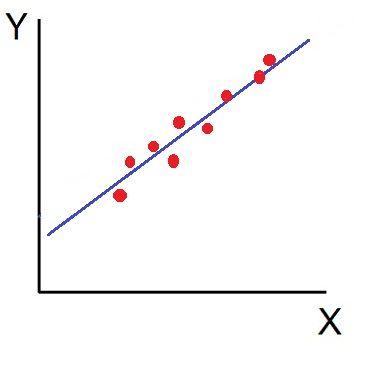
- High Degree of –Ve Correlation (r= – High): The degree of negative correlation is high when the point plotted fall in the narrow band and show the declining tendency from the upper left-hand corner to the lower right-hand corner.
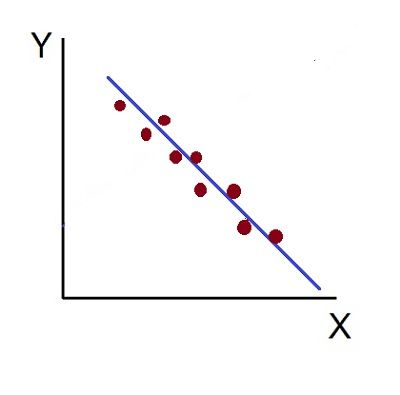
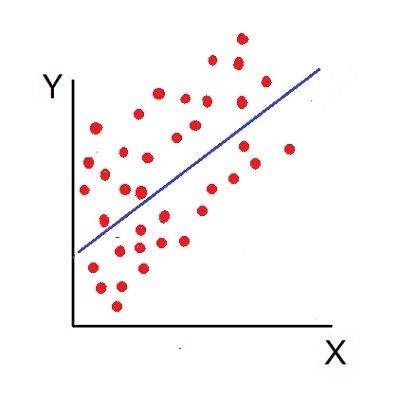
- Low degree of +Ve Correlation (r= + Low): The correlation between the variables is said to be low but positive when the points are highly scattered over the graph and show a rising tendency from the lower left-hand corner to the upper right-hand corner.
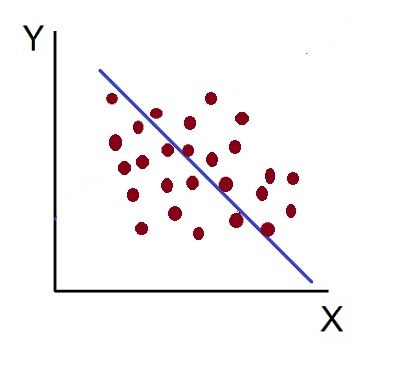
- Low Degree of –Ve Correlation (r= + Low): The degree of correlation is low and negative when the points are scattered over the graph and the show the falling tendency from the upper left-hand corner to the lower right-hand corner.
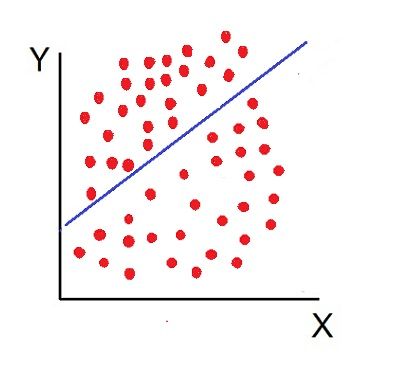
- No Correlation (r= 0): The variable is said to be unrelated when the points are haphazardly scattered over the graph and do not show any specific pattern. Here the correlation is absent and hence r = 0.
Thus, the scatter diagram method is the simplest device to study the degree of relationship between the variables by plotting the dots for each pair of variable values given. The chart on which the dots are plotted is also called as a Dotogram.
Que 1
Que 2
Que 3






